无理数是什么

无理数是什么

无理数是指实数范围内不能表示成两个整数之比的数。简单来说，无理数是无限不循环小数。如圆周率、√2(根号2)等。

无理数与有理数的区别：

实数分为有理数和无理数。有理数和无理数主要区别有两点：

（1）有理数可分为整数(正整数、0、负整数)和分数(正分数、负分数)。把有理数和无理数都写成小数形式时，有理数能写成有限小数或无限循环小数，比如4=4.0；4/5=0.8等等；也可分为正有理数(正整数、正分数)，0，负有理数(负整数、负分数)。

而无理数只能写成无限不循环小数，比如√2=1.4142...，π=3.1415926...，根据这一点，人们把无理数定义为无限不循环小数．

（2）所有的有理数都可以写成两个整数之比，而无理数却不能写成两个整数之比．因此，无理数也叫做非比数。

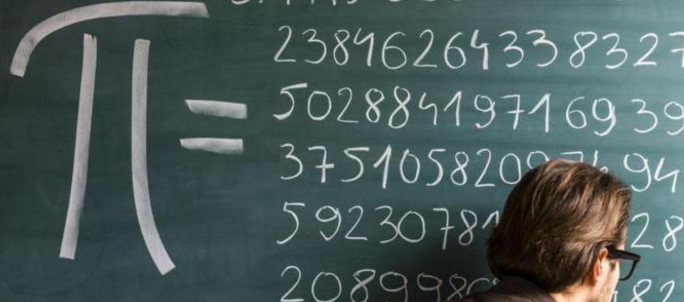
扩展资料：

无理数在位置数字系统中表示（例如，以十进制数字或任何其他自然基础表示）不会终止，也不会重复，即不包含数字的子序列。例如，数字π的十进制表示从3.141592653589793开始，但没有有限数字的数字可以精确地表示π，也不重复。

必须终止或重复的有理数字的十进制扩展的证据不同于终止或重复的十进制扩展必须是有理数的证据，尽管基本而不冗长，但两种证明都需要一些工作。数学家通常不会把“终止或重复”作为有理数概念的定义。

无理数也可以通过非终止的连续分数来处理。

参考资料来源：百度百科-无理数