只能拼图高手进 3*3的图能出现这种情况吗(最后两个相邻的相反的) 怎么解???
的有关信息介绍如下:不可还原的拼图介绍
现在很多手机和电子词典上都有这款游戏,不知到大家在玩的时候有没有发现有的拼图怎么都还原不到完整的图片(或数字顺序),最终出现有1对板块(两个)是对调的,这个时候你可以停下来了,这不是你水平的问题,是游戏设计者的过错!很多游戏设计者都是将板块随机打乱,实际上并不是所有随机打乱之后都是可以还原的!确切的说,随机打乱后,有二分之一的概率是可以被还原的。详细证明如下:
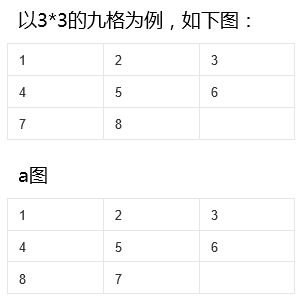
b图
假设图中的a是3*3数字拼图标准的结果,则对于图b的状态是不可能变换成a的。证明起来需要用到高等代数里逆序数的概念,具体的说是用到了一个简单的定理。
定义:在一个1,2,...,n的排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。逆序数为偶数的排列称为偶排列;逆序数为奇数的排列称为奇排列。如2431中,21,43,41,31是逆序,逆序数是4,为偶排列。——这是北大《高等代数》上的定义。
定理:交换一个排列中的两个数,则排列的奇偶性发生改变。(证明见任何一本《高等代数》)
我们将空格看成数字9(数字9对应空位),按正常顺序看a图,9个数字排列是123456789,其逆序数是0,是偶排列;b图是123456879,逆序数是1,是奇排列。我们知道,我们能够移动空块相邻的块,这里的移动相当于一种特殊的对换(相邻对换),例如:对于b图,移动6就相当于9和6互换(9向上移动了),移动7就相当于9和7互换(9向左移动了)。现在假设从b图经过一系列的平移变到了a图,则空格块9必然移动(对换)了偶数次(向左一次必然要再向右一次回来,向上一次必然要向下再回来,最终才能够回到右下角的位置),根据上面的定理最终变成的排列必然是仍然是奇排列(和b相同),然而a图是偶排列,因而产生矛盾,因此b图不可能通过平移变成最终的a图。
呵呵 采纳吧



