黎曼积分的定义

黎曼积分的定义

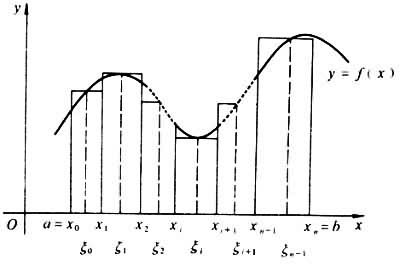
一个闭区间[a,b]的一个分割是指在此区间中取一个有限的点列a=x0<x1<x2<...<xn=b。每个闭区间[xi,xi + 1]叫做一个子区间。定义λ 为这些子区间长度的最大值：λ = max(xi + 1 − xi)，其中0≤i≤n-1。

再定义取样分割。一个闭区间[a,b]的一个取样分割是指在进行分割a=x0<x1<x2<...<xn=b后，于每一个子区间中[xi,xi+ 1]取出一点 xi≤ti≤xi+1。λ的定义同上。

精细化分割：设x0,...,xn以及t0,...,tn-1构成了闭区间[a,b]的一个取样分割，y0,...,ym和s0,...,sm-1是另一个分割。如果对于任意0≤i≤n，都存在r(i)使得xi = yr(i)，并存在使得ti = sj，那么就把分割：y0,...,ym、s0,...,sm-1称作分割x0,...,xn、t0,...,tn-1的一个精细化分割。简单来说，就是说后一个分割是在前一个分割的基础上添加一些分点和标记。

于是我们可以在此区间的所有取样分割中定义一个偏序关系，称作“精细”。如果一个分割是另外一个分割的精细化分割，就说前者比后者更“精细”。 对一个在闭区间[a,b]有定义的实值函数f，f关于取样分割x0,...,xn、t0,...,tn-1的黎曼和定义为以下和式：

和式中的每一项是子区间长度xi + 1 − xi与在ti处的函数值f(ti)的乘积。直观地说，就是以标记点ti到X轴的距离为高，以分割的子区间为长的矩形的面积。