所有自然数之和究竟等于多少?正无穷
的有关信息介绍如下:所有的自然数的个数为无数多个,所以和为无穷大。
自然数集是一个无穷集合,具有无穷性。自然数列可以无止境地写下去。无穷大就是无穷,无穷是不存在,无穷大就是不存在,即所有自然数的和无法统计。
自然数是指表示物体个数的数,即由0开始,0,1,2,3,4,……一个接一个,组成一个无穷的集体,即指非负整数。
扩展资料:
一、自然数的定义:
自然数是指表示物体个数的数,即由0开始,0,1,2,3,4,……一个接一个,组成一个无穷的集体,即指非负整数。
自然数用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4,……所表示的数。表示物体个数的数叫自然数,自然数由0开始,一个接一个,组成一个无穷的集体。自然数有有序性,无限性。分为偶数和奇数,合数和质数等。
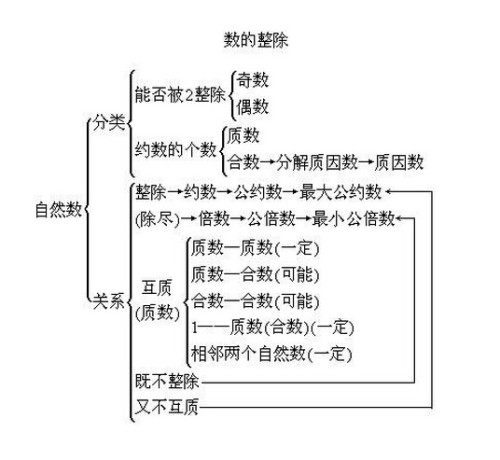
二、自然数的性质:
有序性
自然数的有序性是指,自然数可以从0开始,不重复也不遗漏地排成一个数列:0,1,2,3,…这个数列叫自然数列。一个集合的元素如果能与自然数列或者自然数列的一部分建立一一对应,我们就说这个集合是可数的,否则就说它是不可数的。
2.无限性
自然数集是一个无穷集合,自然数列可以无止境地写下去。
3.对自然数可以定义加法和乘法。其中,加法运算“+”定义为:
a + 0 = a;
a + S(x) = S(a +x), 其中,S(x)表示x的后继者。
3.传递性
设 n1,n2,n3 都是自然数,若 n1>n2,n2>n3,那么 n1>n3。
4.三岐性
对于任意两个自然数n1,n2,有且只有下列三种关系之一:n1>n2,n1=n2或n1<n2。
三、自然数的分类:
按是否是偶数分:可分为奇数和偶数。
奇数:不能被2整除的数叫奇数。
偶数:能被2整除的数叫偶数。也就是说,除了奇数,就是偶数。
注:0是偶数。(2002年国际数学协会规定,零为偶数.我国2004年也规定零为偶数。偶数可以被2整除,0照样可以,只不过得数依然是0而已)。
2.按因数个数分:可分为质数、合数、1和0。
质数:只有1和它本身这两个因数的自然数叫做质数。也称作素数。
合数:除了1和它本身还有其它的因数的自然数叫做合数。
四、自然数的数列:
数列0,1,2,3,4,5,6,7,8,9,10,11,12,……n,称为自然数列。
自然数列的通项公式an=n。
自然数列的前n项和Sn=n(n+1)/2。 Sn=na1+n(n-1)/2
自然数列本质上是一个等差数列,首项a1=1,公差d=1。