aⁿ－bⁿ＝

aⁿ－bⁿ＝

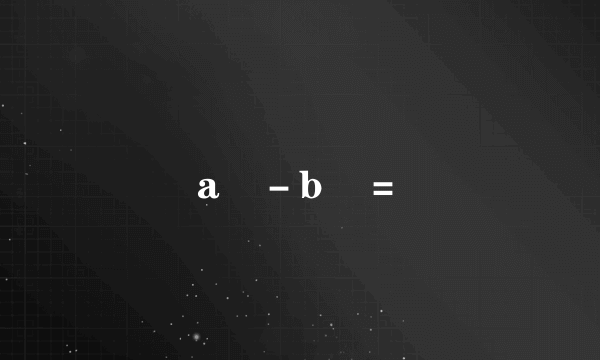
a^n-b^n=a^n-a^(n-1)b+a^(n-1)b-a^(n-2)b^2+a^(n-2)b^2-a^(n-3)b^3+a^(n-3)b^3-……-a^3b^(n-3)+a^3b^(n-3)-a^2b^(n-2)+a^2b^(n-2)-ab^(n-1)+ab^(n-1)-b^n=[a^n-a^(n-1)b]+[a^(n-1)b-a^(n-2)b^2]+[a^(n-2)b^2-a^(n-3)b^3]+[a^(n-3)b^3-……-a^3b^(n-3)]+[a^3b^(n-3)-a^2b^(n-2)]+[a^2b^(n-2)-ab^(n-1)]+[ab^(n-1)-b^n]=(a-b)a^(n-1)+(a-b)a^(n-2)b+(a-b)a^(n-3)b^2+……+(a-b)a^2b^(n-3)+(a-b)ab^(n-2)+(a-b)b^(n-1)=(a-b)[a^(n-1)+a^(n-2)b+a^(n-3)b^2+……+a^2b^(n-3)+ab^(n-2)+b^2]此式就是a^n-b^n的展开式。当n=1时，a^1-b^1=a-bn=2时，=（a-b）（a+b) n=3时, =(a-b)（a^2+ab+b^2）n=4时，=(a-b)(a^3+a^2b+ab^2+b^3)等等。有什么问题请留言。