在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为24cm和30cm的两部分，求三角形得三边长

在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为24cm和30cm的两部分，求三角形得三边长

设AD=DC=a，则AB=2a，设BC=b。

得方程组

2a+a=24

a+b=30

或得方程组

2a+a=30

a+b=24

解得：

a=8 ,b=22,或a=10 ,b=14

所以三边长分别为：

16cm、16cm、22cm或20cm、20cm、14cm

三角形的面积公式：

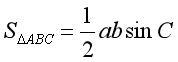
(其中，a、b为三角形两边，C为边c所对角)

因为该公式涉及到建立在直角三角形基础上的正弦值，而“正弦”摆脱圆的控制而在直角三角形中讨论，是16世纪的事。哥白尼的得意门生——奥地利数学家雷提库斯（Rhaeticus，1514—1574）在《三角学准则》一书中，将正弦函数的定义直接建立在“直角三角形”上，即sinα=对边/斜边。因此，可断定出现在16世纪以后。