导线截面积怎么得来的

导线截面积怎么得来的

单根导线截面积=导线直径的平方乘以0.7854

一般铜导线载流量导线的安全载流量是根据所允许的线芯最高温度、冷却条件、敷设条件来确定的。一般铜导线的安全载流量为5~8A/mm2，铝导线的安全载流量为3~5A/mm2。 <关键点> 一般铜导线的安全载流量为5~8A/mm2，铝导线的安全载流量为3~5A/mm2。

如：2.5 mm2 BVV铜导线安全载流量的推荐值2.5×8A/mm2=20A 4 mm2 BVV铜导线安全载流量的推荐值4×8A/mm2=32A 二、计算铜导线截面积利用铜导线的安全载流量的推荐值5~8A/mm2。

计算出所选取铜导线截面积S的上下范围： S=< I /（5~8）>=0.125 I ~0.2 I（mm2） S-----铜导线截面积（mm2） I-----负载电流（A） 三、功率计算一般负载（也可以成为用电器，如点灯、冰箱等等）分为两种，一种式电阻性负载，一种是电感性负载。

对于电阻性负载的计算公式：P=UI 对于日光灯负载的计算公式：P=UIcosф，其中日光灯负载的功率因数cosф=0.5。

拓展资料：

一物体以特定角度观看时的截面积是该物体在此角度下正交投影的总面积。例如一高为h，半径为r的圆柱，若沿着其中心轴，其截面积

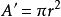
若沿着任一个和中心轴垂直的线，其截面积

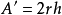
一个半径为r的球体，在任意角度下的截面积均为

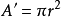
一物体的截面积可由下式的曲面积分求得：

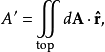
祖暅原理，又名等幂等积定理，是指所有等高处横截面积相等的两个同高立体，其体积也必然相等的定理。祖暅之《缀术》有云：“缘幂势既同，则积不容异。”

该原理最早由中国古代数学家刘徽提出。南北朝时又被祖冲之的儿子祖暅提出。祖冲之两父子采用这一原理，求出了牟合方盖的体积，进而算出球体积。在欧洲17世纪意大利数学家卡瓦列里亦发现相同定理，所以西方文献一般称该原理为卡瓦列里原理。

在现代的解析几何和测度应用中，祖暅原理是富比尼定理中的一个特例。卡瓦列里没有对这条的严谨证明，只发表在1635年的Geometria indivisibilibus以及1647年的Exercitationes Geometricae中，用以证明自己的Methode der Indivisibilien。

以此方式可以计算某些立体的体积，甚至超越了阿基米德和开普勒的成绩。这个定理引发了以面积计算体积的方法并成为了积分发展的一个重要步骤。