三角形边长是什么？

三角形边长是什么？

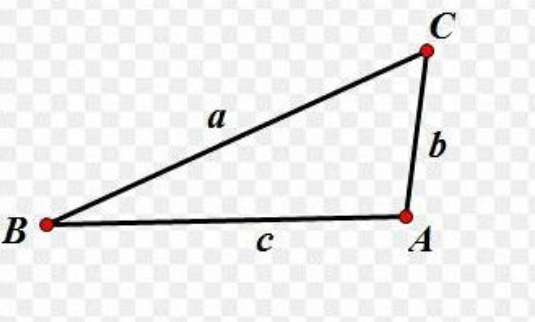
求三角形的边长的公式：cosA=(b^2＋c^2－a^2)/2bc； cosB=(a^2＋c^2－b^2)/2ac； cosC=(a^2＋b^2－c^2)/2ab 也就是余弦定理。

根据已知条件和三角函数定义有：

tanA=BC/AB

即，BC=AB*tanA=AB*tan5(度)=8*0.08748

故，BC=0.6998=0.7

又，cosA=AB/AC

即，AC=AB/cosA=8/cos5=8/0.9962=8.03

直角三角形：

性质1：直角三角形两直角边的平方和等于斜边的平方。

性质2：在直角三角形中，两个锐角互余。

性质3：在直角三角形中，斜边上的中线等于斜边的一半。

性质4：直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。　性质5:如图3，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：

（1） AD^2=BD·DC。

（2） AB^2=BD·BC射影定理图。

（3） AC^2=CD·BC等积式。

（4）ABXAC=ADXBC (可用面积来证明）。

直角三角形的外接圆的半径R=1/2BC,直角三角形的内切圆的半径r=1/2(AB+AC-BC)(公式一)；r=AB*AC/(AB+BC+CA)。