曲率半径如何计算

曲率半径如何计算

在空间曲线的情况下，曲率半径是曲率向量的长度。在平面曲线的情况下，则R要取绝对值。

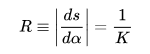
其中s是曲线上固定点的弧长，α是切向角，K是曲率。

如果曲线以笛卡尔坐标表示为y（x） ，则曲率半径为（假设曲线可微分）：

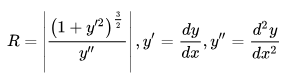
如果曲线由函数x（t）和y（t）参数给出，则曲率为：

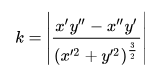
如果：

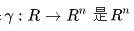
中的参数曲线，则曲线各点处的曲率半径

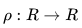
由下式给出：

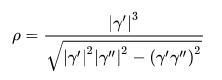
具体应用

（1）对于差分几何上的应用，请参阅Cesàro方程；

（2）对于地球的曲率半径（由椭圆椭圆近似），请参见地球的曲率半径；

（3）曲率半径也用于梁的弯曲三部分方程中；

（4）曲率半径（光学）。

（5）半导体结构中的应力：

涉及蒸发薄膜的半导体结构中的应力通常来自制造过程中的热膨胀（热应力）。发生热应力是因为膜沉积通常在室温以上。在从沉积温度冷却至室温时，基板和膜的热膨胀系数的差异引起热应力。