lnx的函数图像是什么样子的

lnx的函数图像是什么样子的

lnx的函数图像如下图所示：

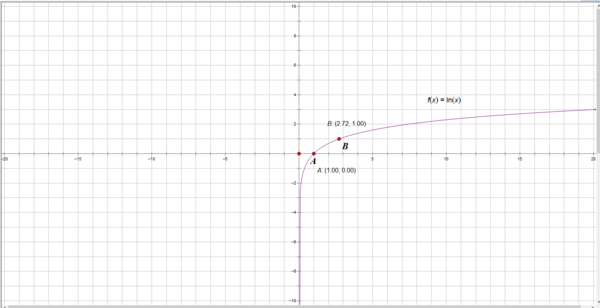
ln为一个算符，意思是求自然对数，即以e为底的对数。

e是一个常数，等于2.71828183…

lnx可以理解为ln(x)，即以e为底x的对数，也就是求e的多少次方等于x。

lnx=loge^x

扩展资料：

自然对数lnx的发展历史：

在1614年开始有对数概念，约翰·纳皮尔以及Jost Bürgi（英语：Jost Bürgi）在6年后，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数，当时还没出现有理数幂的概念。

1742年William Jones（英语：William Jones (mathematician)）才发表了幂指数概念。按后来人的观点，Jost Bürgi的底数1.0001相当接近自然对数的底数e，而约翰·纳皮尔的底数0.99999999相当接近1/e。

实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，Henry Briggs（英语：Henry Briggs (mathematician)）建议纳皮尔改用10为底数未果，他用自己的方法于1624年部份完成了常用对数表的编制。